ABC382(A-F)

题目大意

有 \(N\) 个盒子，给你一个长度为 \(N\) 的字符串 \(S\)，如果 \(S_i\) 是 @，表示第 \(i\) 个盒子有一块饼干，如果 \(S_i\) 是 .，表示第 \(i\) 个盒子是空的。如果吃掉 \(D\) 块饼干（保证 \(N\) 个盒子中至少有 \(D\) 块饼干），还剩多少块饼干？

参考代码

C++

#include <algorithm>
#include <iostream>
#include <string>

using namespace std;

int main()
{
    int n, d;
    string s;
    cin >> n >> d >> s;
    int cnt = count(s.begin(), s.end(), '.');
    cout << cnt + d << endl;
    return 0;
}

题目大意

有 \(N\) 个盒子，给你一个长度为 \(N\) 的字符串 \(S\)，如果 \(S_i\) 是 @，表示第 \(i\) 个盒子有一块饼干，如果 \(S_i\) 是 .，表示第 \(i\) 个盒子是空的。有人打算吃掉 \(D\) 块饼干（保证 \(N\) 个盒子中至少有 \(D\) 块饼干），他每一次会选择最靠右且有饼干的盒子，吃掉其中的饼干。在他吃掉 \(D\) 块饼干后，从左到右输出 \(N\) 个盒子是否有饼干。

参考代码

C++

#include <iostream>
#include <string>

using namespace std;

int main()
{
    int n, d;
    string s;
    cin >> n >> d >> s;
    for(int i = n - 1; i >= 0 && d; i--)
        if(s[i] == '@')
        {
            d--;
            s[i] = '.';
        }
    cout << s << endl;
    return 0;
}

C - Kaiten Sushi ¶

题目大意

有 \(N(1 \le N \le 2 \times 10 ^ 5)\) 去吃寿司，不同的寿司有不同的美味度，第 \(i\) 个人对寿司美味度的要求是至少为 \(A_i\)，即，如果第 \(i\) 个人看见了美味度大于等于 \(A_i\) 的寿司，就会吃掉。

这 \(N\) 个人从左到右（第 \(1\) 个人在最左，第 \(N\) 个人在最右）坐成一行，寿司在传送带上，传送带的方向是从左到右的，因此寿司总是先被第 \(1\) 个人看见。一共有 \(M(1 \le M \le 2 \times 10 ^ 5)\) 个寿司，第 \(i\) 个寿司的美味度是 \(B_i\)。如果第 \(i\) 个人看见了美味度大于等于 \(A_i\) 的寿司，就会吃掉这个寿司，被吃掉的寿司不会被后面的人看见。如果第 \(i\) 个人看见了美味度小于 \(A_i\) 的寿司，会无视掉这个寿司，随后这个寿司将被下一个人看见。每个人可以吃下无数个寿司。

问：这个 \(M\) 个寿司分别是被谁吃下的？按顺序输出第 \(i\) 个寿司是被哪个人吃下的。（如果某个寿司没有任何人吃，输出 -1）

解题思路

第 \(i\) 个人的美味度要求是 \(A_i\)，则所有美味度大于等于 \(A_i\) 的寿司都会被他吃掉，因此后面大于等于 \(A_i\) 的人都会被屏蔽掉。所以只需要从 \(A_i\) 开始，求出连续递减的子序列，则只有这个子序列的人会吃到寿司。

参考代码

C++

#include <functional>
#include <iostream>
#include <limits>
#include <map>

using namespace std;

int main()
{
    int n, m;
    cin >> n >> m;
    map<int, int, greater<int>> pos;
    for (int i = 1, last = numeric_limits<int>::max(); i <= n; i++)
    {
        int a;
        cin >> a;
        if(a < last)
        {
            pos[a] = i;
            last = a;
        }
    }
    while (m--)
    {
        int b;
        cin >> b;
        auto it = pos.lower_bound(b);
        cout << (it == pos.end() ? -1 : it->second) << endl;
    }
    return 0;
}

D - Keep Distance ¶

题目大意

给你两个整数 \(N(2 \le N \le 12)\) 和 \(M(10N-9 \le M \le 10N)\)

按照字典序输出所有满足以下条件的序列 \((A_1, A_2, ..., A_N)\)：

\(1 \le A_i\)
对于所有的 \(i \in [2, N]\)，有 \(A_{i-1} + 10 \le A_i\)
\(A_N \le M\)

解题思路

dfs 模板题。

参考代码

C++

#include <iostream>
#include <vector>

using namespace std;

int main()
{
    int n, m;
    cin >> n >> m;
    vector<vector<int>> ans;
    vector<int> now(n);

    auto dfs = [&ans, &now, n, m](auto &self, int cur, int last) -> void
    {
        if (cur == n)
        {
            ans.push_back(now);
            return;
        }

        int cnt = n - cur - 1;
        for (int i = last; i + 10 * cnt <= m; i++)
        {
            now[cur] = i;
            self(self, cur + 1, 10 + i);
        }
    };

    dfs(dfs, 0, 1);
    cout << ans.size() << endl;
    for(auto &v : ans)
    {
        for(auto x : v)
            cout << x << ' ';
        cout << endl;
    }
    return 0;
}

E - Expansion Packs ¶

题目大意

有无限多个卡包，每个卡包有 \(N(1 \le N \le 5000)\) 张卡。在每个卡包中，第 \(i\) 张卡有 \(P_i\%\) 的概率是稀有卡，其中 \(1 \le P_i \le 100\)。每张卡是否稀有相互独立。

你将一直打开新卡包，并获得每个打开的卡包中的所有卡，直到累计获得至少 \(X(1 \le X \le 5000)\) 张稀有卡为止。

问：当你停下时，打开的卡包数量的数学期望是多少？

解题思路

因为每个卡包内的每一张卡的稀有概率是固定的，可以处理出一个 \(g[i][j]\) 表示在一个卡包的前 \(i\) 张卡中开出 \(j\) 张稀有卡的概率，显然有 \(g[i][j] = g[i][j] \times \frac{100-P_i}{100} + g[i-1][j-1] \times \frac{P_i}{100}\)，可以在 \(O(N^2)\) 的时间预处理出来，则 \(g[N][j]\) 就表示开一个卡包获得 \(j\) 张稀有卡的概率。

设 \(dp[i]\) 表示累计获得至少 \(i\) 张稀有卡需要打开卡包数量的数学期望，初始的时候有 \(dp[0] = 0\)，转移时，枚举新打开一个卡包能获得多少张稀有卡，一个卡包有 \(N\) 张卡，最多可获得 \(N\) 张稀有卡，最少获得 \(0\) 张，因此枚举 \(0 \le j \le N\)，即：\(dp[i] = 1 + \sum\limits_{j=0}^Ndp[i-j]g[N][j]\)

然后我们会发现两个问题，首先 \(i-j\) 是有可能小于 \(0\) 的，这可以通过 \(\max(i-j, 0)\) 避免，也就时 \(dp[i] = 1 + \sum\limits_{j=0}^Ndp[\max(i-j, 0)]g[N][j]\)，另一个问题是，当 \(j = 0\) 时，右式会出现 \(dp[i]\)，但是这个式子就是为了求出 \(dp[i]\) 的，所以我们变换一下：

\[ \begin{align*} dp[i] & = 1 + \sum\limits_{j=0}^Ndp[\max(i-j, 0)]g[N][j] \\ dp[i] & = 1 + \sum\limits_{j=1}^Ndp[\max(i-j, 0)]g[N][j] + dp[i]g[N][0] \\ (1-g[N][0])dp[i] & = 1 + \sum\limits_{j=1}^Ndp[\max(i-j, 0)]g[N][j] \\ dp[i] & = \frac{1 + \sum\limits_{j=1}^Ndp[\max(i-j, 0)]g[N][j]}{1-g[N][0]} \\ \end{align*} \]

又因为 \(1 \le p \le 100\)，所以 \(g[N][0]\) 一定不等于 \(1\)，因此这个变换是合法的。这样就能算了，预处理 \(g\) 的时间复杂度是 \(O(N^2)\)，计算 \(dp\) 的时间复杂度是 \(O(NX)\)，总复杂度就是 \(O(N^2+NX)\)

参考代码

C++

#include <iomanip>
#include <iostream>
#include <vector>

using namespace std;

int main()
{
    int n, x;
    cin >> n >> x;
    vector<double> g(n+1);
    g[0] = 1;
    for(int i = 1; i <= n; i++)
    {
        double p;
        cin >> p;
        for(int j = i; j; j--)
            g[j] = g[j] * (100-p)/100 + g[j-1] * p / 100;
        g[0] *= (100-p)/100;
    }
    vector<double> dp(x+1);
    for(int i = 1; i <= x; i++)
    {
        double sum = 1;
        for(int j = 1; j <= n; j++)
            sum += dp[max(i-j, 0)] * g[j];
        dp[i] = sum / (1 - g[0]);
    }
    cout << setprecision(8) << dp[x] << endl;
    return 0;
}

F - Falling Bars ¶

题目大意

有一个 \(H \times W(1 \le H, W \le 2 \times 10 ^ 5)\) 的网格。网格中有 \(N(1 \le N \le 2 \times 10 ^ 5)\) 个高度为 \(1\) 格的方块，每个方块的初始位置用三个数字 \((R_i, C_i, L_i)\) 来描述，表示这个方块占据了 \((R_i, C_i), (R_i, C_i+1), ..., (R_i, C_i+L-1)\) 的位置。输入数据保证这 \(N\) 个方块是不重叠的。

初始的时间是 \(t=0\)，在每个 \(t=0.5+n\)（其中 \(n\) 表示自然数）的时刻，会发生以下事情：

首先，按顺序遍历所有的方块，对于所有的 \(i = 1, 2, ..., N\)，假设第 \(i\) 个方块当前的位置是 \((R_i, C_i), (R_i, C_i+1), ..., (R_i, C_i+L-1)\)，如果 \(R_i + 1 \le W\)，且 \((R_i+1, C_i), (R_i + 1, C_i+1), ..., (R_i + 1, C_i+L-1)\) 都没有被占据，则第 \(i\) 个方块整体向下移动 \(1\) 格，占据这些位置。即：如果第 \(i\) 个方块没有到达网格的底部，且方块下方 \(1\) 格没有被占据，就整体下移 \(1\) 格。
否则，如果第 \(i\) 个方块处于网格的底部，或者其下方 \(1\) 格的位置被占据，则跳过第 \(i\) 个方块的操作。

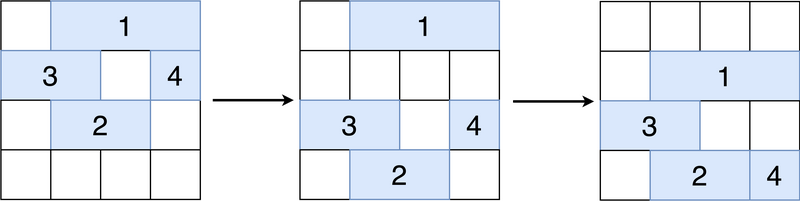
问：在 \(t = 10^{100}\)，这 \(N\) 个方块的 \(R_i\) 分别是多少？例子见上图。

解题思路

可以发现，像上图的这样的情况，无论这个网格有多大，第 \(2\) 个方块都会保持在最底端，所以为了加快计算，不能一格一格的移动，应该一次性移动多格。为了移动多格，我们需要算出某一段最高的可被覆盖的位置，这可以用线段树维护一个区间最小值实现。

具体来说，我们用 \(h[i]\) 表示第 \(i\) 列最上方未被占据的行号，初始值就是 \(h[i] = W\)，当某个方块下落时，假设当前方块占据的是 \((R_i, C_i), (R_i, C_i+1), ..., (R_i, C_i+L-1)\)，就查询 \(h[C_i]\) 到 \(h[C_i + L_i - 1]\) 这一个区间的最小值，模拟下落被卡住的情况。确定下落的位置后，方块占据这一段，因此这一段的值也要修改，涉及到区间修改和区间最小值查询，所以用线段树维护这个 \(h\) 数组即可。

实际操作的时候，还可以注意到，一定是越靠近底部的方块先确定最终位置，所以按照 \(R_i\) 降序排序即可，这样每一次操作都可以确定一个方块的最终位置，一共 \(N\) 个方块，单次线段树的修改和查询操作时间复杂度是 \(O(\log W)\)，因此总的时间复杂度就是 \(O(N\log W)\)

参考代码

C++

#include <algorithm>
#include <iostream>
#include <limits>
#include <vector>

using namespace std;

struct SegTree
{
    struct Node
    {
        int m;
        bool lazy = false;
        Node(int x) : m(x) {}
    };

    vector<Node> t;

    SegTree(int n, int val) : t(4 * n, val) {}

    void push_down(int p)
    {
        if (t[p].lazy)
        {
            int lch = p * 2, rch = p * 2 + 1;
            t[lch].m = t[rch].m = t[p].m;
            t[lch].lazy = t[rch].lazy = true;
            t[p].lazy = false;
        }
    }

    int query(int p, int beg, int end, int l, int r)
    {
        if (end < l || beg > r)
            return numeric_limits<int>::max();
        if (beg >= l && end <= r)
            return t[p].m;
        push_down(p);
        int mid = (beg + end) / 2;
        int lch = p * 2, rch = p * 2 + 1;
        return min(query(lch, beg, mid, l, r), query(rch, mid + 1, end, l, r));
    }

    void update(int p, int beg, int end, int l, int r, int x)
    {
        if (end < l || beg > r)
            return;
        if (beg >= l && end <= r)
        {
            t[p].m = x;
            t[p].lazy = true;
            return;
        }
        push_down(p);
        int mid = (beg + end) / 2;
        int lch = p * 2, rch = p * 2 + 1;
        update(lch, beg, mid, l, r, x);
        update(rch, mid + 1, end, l, r, x);
        t[p].m = min(t[p].m, x);
    }
};

struct Bar
{
    int depth, left, right, id;
};

int main()
{
    int h, w, n;
    cin >> h >> w >> n;
    SegTree t(w, h);
    vector<Bar> bars(n);
    for (int i = 0; i < n; i++)
    {
        int r, c, l;
        cin >> r >> c >> l;
        bars[i] = {r, c, c + l - 1, i};
    }
    sort(bars.begin(), bars.end(), [](const Bar &x, const Bar &y) -> bool
         { return x.depth > y.depth; });
    vector<int> ans(n);
    for (auto b : bars)
    {
        int m = t.query(1, 1, w, b.left, b.right);
        ans[b.id] = m;
        t.update(1, 1, w, b.left, b.right, m - 1);
    }
    for (auto x : ans)
        cout << x << endl;
    return 0;
}

最后更新: 2024-12-31
创建日期: 2024-12-31

ABC382(A-F)

A - Daily Cookie¶

B - Daily Cookie 2¶

C - Kaiten Sushi¶

D - Keep Distance¶

E - Expansion Packs¶

F - Falling Bars¶

A - Daily Cookie ¶

B - Daily Cookie 2 ¶

C - Kaiten Sushi ¶

D - Keep Distance ¶

E - Expansion Packs ¶

F - Falling Bars ¶